Downloads
Software and movies and still pictures and lectures are
available for downloading. They should be useable in several opearating systems.
 Version
II_III of the perspex machine is implemented in Pop11.
It can be run on both Microsoft and Unix operating
systems. This version of the machine was used to develop the examples in
the papers Perspex Machine II
and Perspex Machine III.
It does not have documentation. It is not a generic implementation of the perspex
machine. It will be of use only to skilled programmers.
Isabelle/HOL proof files supporting the
paper Perspex Machine VIII.
This code will be of use only to mathematicians familiar with Isabelle/HOL.
Source code and documentation supporting the
paper Perspex Machine XII. This provides an implementation of transcomplex arithmetic in Pop11 along with various examples, including the computation of singular physical properties.
FibonacciPerspex
shows a perspex neural net compiled from a C
program that calculates the first ten Fibonacci numbers.
void main() {double i, j, k, l; i = 0; j = 1; k = 1; l = 0; for (l = 0; l
< 10; l = l + 1) {k = i + j; i = j; j = k;} k = k;}
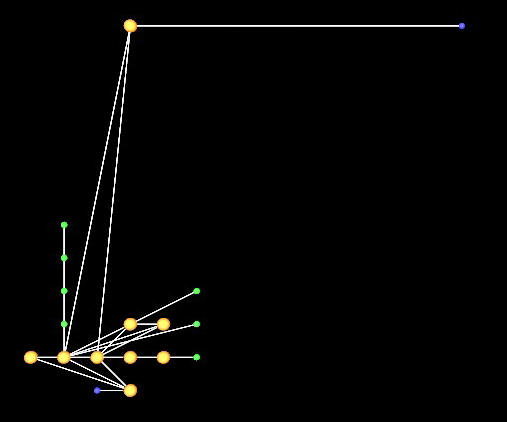 The
first frame of the movie shows the initial condition of the neural net. The
neurons are shown in the standard perspex colours: read synapses red, body
orange, write synapse green, and jump synapses blue. Processing starts in
the bottom left of the net. The neuron at the top left controls the number
of Fibonacci numbers that are computed. Moving this neuron higher up causes
the net to compute more Fibonacci numbers, lowering it causes the net to
compute fewer Fibonacci numbers. The net starts by growing some local
variables vertically upwards on the left hand side. It then grows each
Fibonacci number rightward, storing the result in one of the local
variables. When the net halts this variable holds the tenth Fibonacci
number.
In principle, any C program can be compiled into a perspex neural net. The
program then inherits the properties of perspex neural nets but, unless
these are accessed, it executes exactly what the C source program
instructed.
If the neural net were modified in some way, say, by applying filtering or
a genetic algorithm, the result would be a new program related to the
computation of Fibonacci numbers. If the modification were extreme the
relationship would be tenuous.
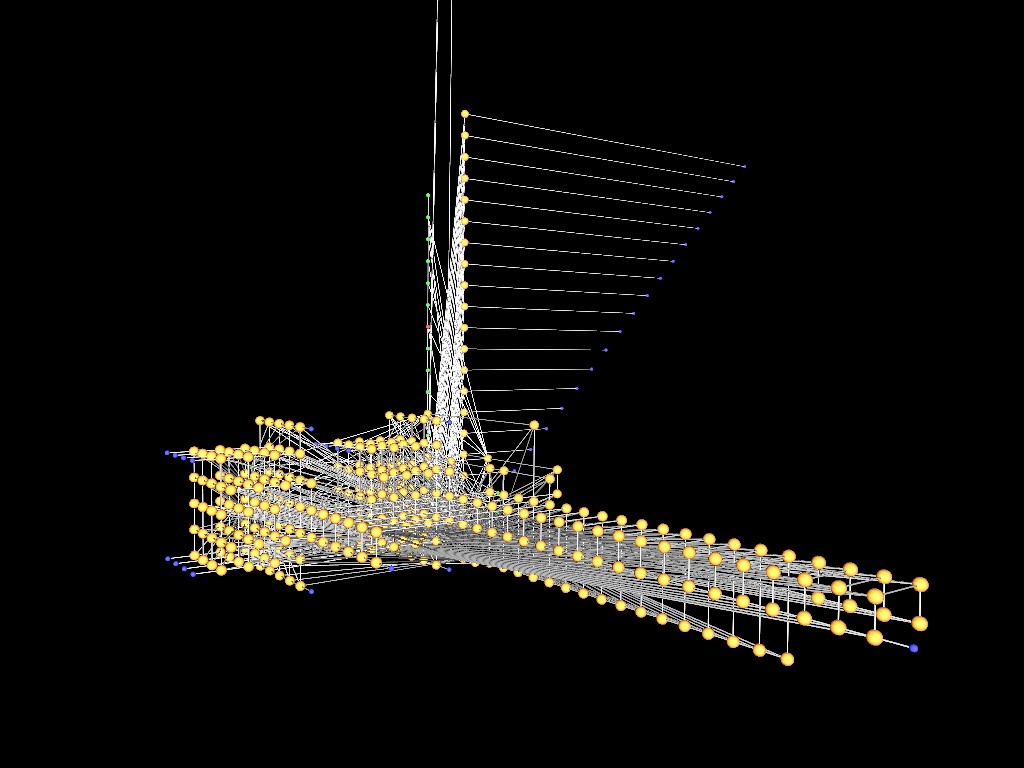
DijkstraPerspex
shows a net with over 600 perspex neurons that
implements Dijkstra's solution to the Travelling Salesman problem. This net
was compiled from the C source code for
Dijkstra's algorithm.
The movie shows the entire net with
all but the recently used neurons fading out over time. When the net halts
it has correctly computed the shortest distance between the cities visited
by the travelling salesman.
The vertical part is mostly local variables. The cubical block of neurons
to the left is the arrays used to hold data about the position of cities.
The fibres to the right are mostly the evaluation function. The answer is
recorded in one of the local variables.
All of these pictures are supplied without
copyright constraint, except that where the photographer is identified, the
photographer wishes to assert the moral right to be identified in all
derivative works.
 James
Anderson beside the Hopkins Building at The
University of Reading, 2009. Photographer: Design
and Print, The University of Reading.
 The Hopkins Building is named after a Physicist
at The University of Reading who
invented the endoscope. This building does not hold the Thames Blue supercomputer,
but it is the kind of building that could. It has a large power supply, air
conditioning, and good physical security.
 James Anderson
beside the Thames Blue
supercomputer, at The University of
Reading, 2009. Photographer: Design and Print, The University of Reading.
The super computer fills a very large room.
 James Anderson
beside the Thames Blue
supercomputer, at The University of
Reading, 2009. Photographer: Design and Print, The University of Reading.
The super computer has a lot of communication cables to send data between
computer cabinets.
 James Anderson
beside the Thames Blue
supercomputer, at The University of
Reading, 2009. Photographer: Design and Print, The University of Reading.
The super computer can be monitored from a single computer cabinet.
 James Anderson
beside Old Whiteknights House at The
University of Reading, 2009. Photographer: Design
and Print, The University of Reading. With a little
thought, one can design transreal computers that have rather more
processors than a conventional computer.
The first generation of transreal Perspex
machines is likely to have one thousand times the number of processors of a
conventional computer. The second generation is likely to have one million
times the number of processors.
Second generation Perspex chips could be used
to build a 128 G processor machine. That is one processor for every neuron
in the human brain. Such a machine will consume about 100 MW of electrical
power, but its processors will run about one million times faster than the
electrical spikes that run between neurons. Does that give the machine one
million times the computational power of a human brain? Who knows? But one
million people consume about 100 MW of power when they are at rest so, in
terms of raw physical power, the figures stack up.
It would be a good idea to build a 128 G
processor machine next to a hydroelectric power station so that it can get
carbon-neutral power and can dispose of its waste heat without using cooling towers.
A final-year undergraduate module in Transcomputation started in 2017 at the University of Reading, England. The lectures were given in ten of two hour blocks. The first hour of every block was a lecture and the second hour was either an exercise class or seminar to reinforce the lecture. Hence only some of the lectures below are accompanied by exercise sheets. Many of the exercises have answer sheets but some of the exercises were entirely open ended so have no answer sheet.
Lecture 1 and Excercise 1 and Answers 1 Introduction and Transreal Arithmetic.
Lecture 2 and Excercise 2 and Answers 2 Relations Operators and Graph Sketching.
Lecture 3 and Excercise 3 Trans-Two's Complement and Transfloat.
Lecture 4 and Excercise 4 and Answers 4 Equations, Functions and Gradient.
Lecture 5 and Excercise 5 and Answers 5 Rotation, Angle and Transcomplex Numbers.
Lecture 6 and Excercise 6 and Answers 6 Transvectors and Transcomplex Arithmetic.
Lecture 7 and Excercise 7 Trans-Newtonian Physics.
Lecture 8 and Excercise 8 and Answers 8 Logic, Sets and Antinomies.
Lecture 9 and Excercise 9 Hardware and Software.
Lecture 10 Revision.
The lecture course was terminated after one run. With its termination, all teaching of the transsciences, in the United Kingdom, was terminated in 2018. Therefater only public lectures were given.
Public Lecture for Secondary Schools.
Presentation to Reading University's Computer Science departmental staff on Monday 13 May 2019.
| 
